AE-02 COVID vaccine and deaths from Delta variant

Application exercise

Goals

Create data visualizations and calculate summary statistics for comparing trends across groups
Distinguishing observational studies and experiments
Identifying confounding variables and understanding Simpson’s paradox

R Goals

In addition to using ggplot to produce graphs, some new R commands that we’ll use in this AE are: count, group_by, mutate, filter, select.

Packages

The tidyverse package contains many of the commands listed above which make working with data easier.

library(tidyverse)

Data

The data for this case study come from a technical briefing published by Public Health England in August 2021 on COVID cases, vaccinations, and deaths from the Delta variant. Each observation is a patient visiting emergency care. Rather than loading an R package that contains this data, we will import the data directly from a file.

delta <- read_csv("delta.csv")

Rows: 268166 Columns: 3
── Column specification ────────────────────────────────────────────────────────
Delimiter: ","
chr (3): vaccine, age, outcome

ℹ Use `spec()` to retrieve the full column specification for this data.
ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.

Task

Use either print or glimpse in the code block below to take a quick look at the data set.

# add code here

Understanding the data

Question 1

How many rows and columns are in this dataset? What do the rows represent? What are the variables and what type are they?

(write your answer here)

Notice that to answer this question, you had to first run the print or glimpse command. This might seem a bit clumsy, but turns out we can incorporate code to get the answers to these qestions directly into our narrative. This is done with inline code, shown here:

There are 268166 rows and 3 columns in the dataset.

When you render this document, the correct values will be inserted into the appropriate place!

Question 2

Do these data come from an observational study or experiment? Why?

(write your answer here)

Visualizing categorical data

To start understanding this data, let’s create a visualization of health outcome by vaccine status that will allow us to compare the proportion of deaths across those who are and are not vaccinated.

ggplot(delta, aes(x = vaccine, fill = outcome)) +
  geom_bar(position = "fill")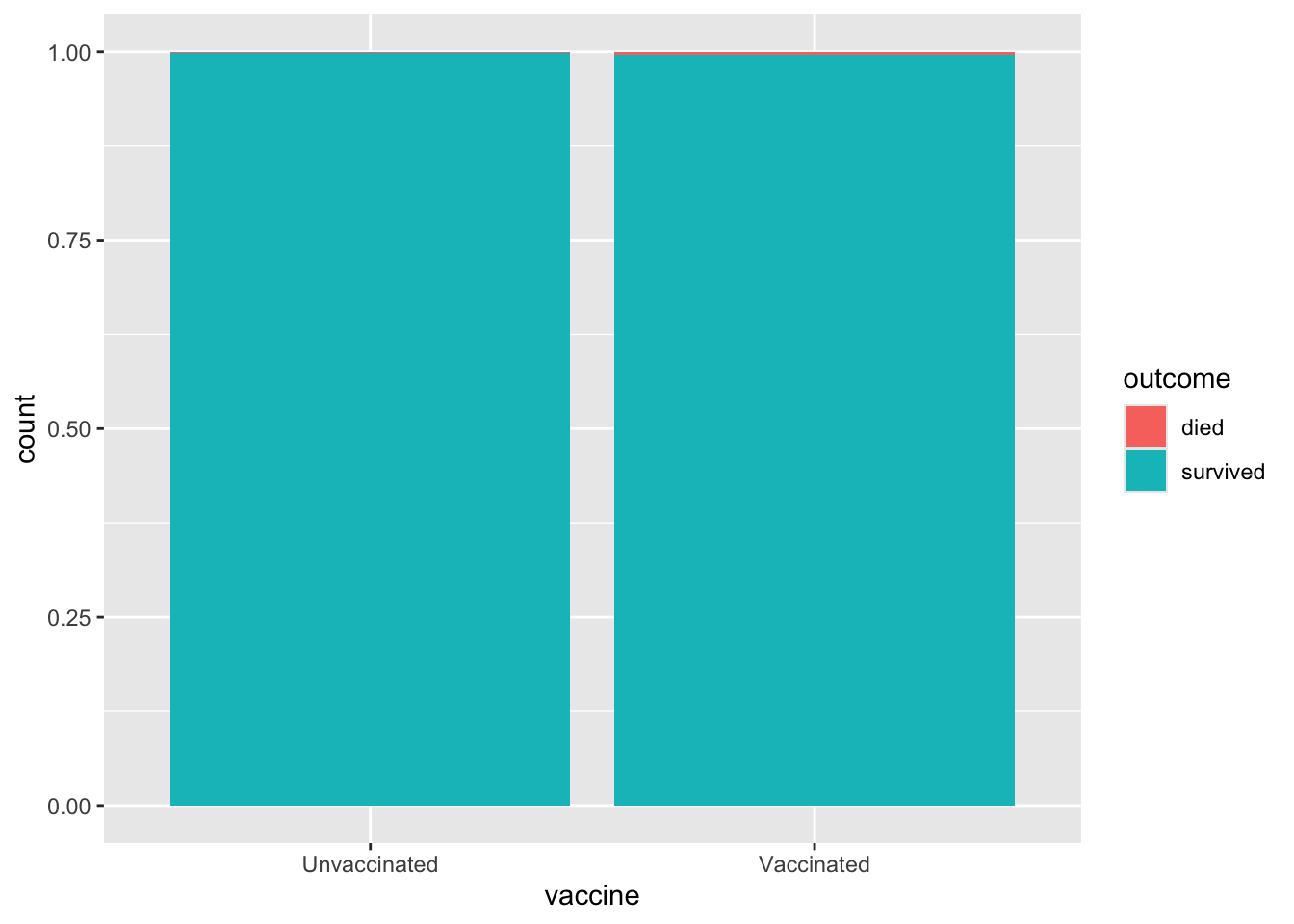

Question 3

What can you say (if anything) about death rates in these two groups based on this visualization?

(write your answer here)

Summarizing catagorical data

You may have noticed that it’s difficult to see any difference between the two groups from this bar graph. So instead, let’s calculate the actual proportions. To do this, we need to know how many vaccinated patients died and how many unvaccinated patients died. Once we have those numbers, we can calculate proportions.

delta |>
  count(vaccine, outcome)

# A tibble: 4 × 3
  vaccine      outcome       n
  <chr>        <chr>     <int>
1 Unvaccinated died        250
2 Unvaccinated survived 150802
3 Vaccinated   died        477
4 Vaccinated   survived 116637

Question 4

Based on the output of this R code, what proportion the vaccinated group died? What proportion of the unvaccinated group died?

(write your answer here)

At heart, R is a fancy calculator, so there’s no reason we can’t ask it to do these calculations for us! The following code does this and adds a new column to the output with these values.

delta |>
  count(vaccine, outcome) |>
  group_by(vaccine) |>
  mutate(prop = n / sum(n))

# A tibble: 4 × 4
# Groups:   vaccine [2]
  vaccine      outcome       n    prop
  <chr>        <chr>     <int>   <dbl>
1 Unvaccinated died        250 0.00166
2 Unvaccinated survived 150802 0.998  
3 Vaccinated   died        477 0.00407
4 Vaccinated   survived 116637 0.996

Question 5

Verify that the proportions you calculated in Question 4 are the same as the values shown on this table.

Improved Visualization and Summary

Our next step is to investigate how controlling for an additional variable changes our understanding of the data. In particular, we want to control for age.

First, a visualization. These are the same as before, except that we get two separate graphs where the data has been separated (faceted) by the age variable.

ggplot(delta, aes(x = vaccine, fill = outcome)) +
  geom_bar(position = "fill") +
  facet_wrap(~age)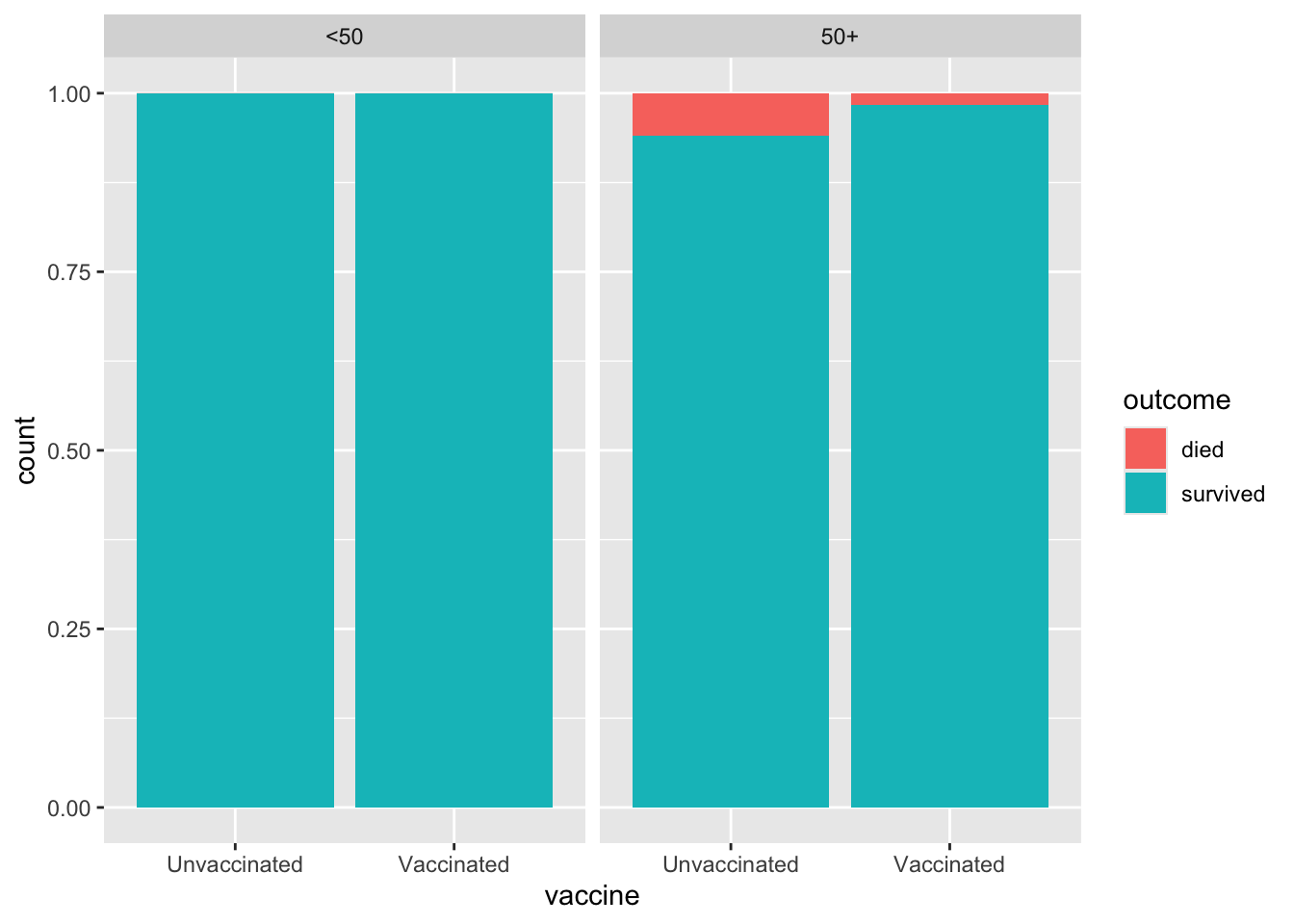

Question 6

What do you notice in these bar graphs?

(write your response here)

Next, we calculate the numerical proportions. This time, there’s an additional variable we’re using to group the population.

delta |>
  count(age, vaccine, outcome) |>
  group_by(age, vaccine) |>
  mutate(prop = n / sum(n))

# A tibble: 8 × 5
# Groups:   age, vaccine [4]
  age   vaccine      outcome       n     prop
  <chr> <chr>        <chr>     <int>    <dbl>
1 50+   Unvaccinated died        205 0.0596  
2 50+   Unvaccinated survived   3235 0.940   
3 50+   Vaccinated   died        459 0.0168  
4 50+   Vaccinated   survived  26848 0.983   
5 <50   Unvaccinated died         45 0.000305
6 <50   Unvaccinated survived 147567 1.00    
7 <50   Vaccinated   died         18 0.000200
8 <50   Vaccinated   survived  89789 1.00

Question 7

what do you notice?

(write your responses here)

Question 8

Based on your findings so far, fill in the blanks with more, less, or equally: Is there anything surprising about these statements? Speculate on what, if anything, the discrepancy might be due to.

In 2021, among those in the UK who were COVID Delta cases, the unvaccinated were _____ likely to die than the vaccinated.
For those under 50, those who were unvaccinated were ____ likely to die than those who were vaccinated.
For those 50 and up, those who were unvaccinated were ____ likely to die than those who were vaccinated.

Simpson’s Paradox

Simpson’s paradox is a phenomenon in which a trend appears in subsets of the data, but disappears or reverses when the subsets are combined. The paradox can be resolved when confounding variables and causal relations are appropriately addressed in the analysis.

Question 9

Let’s rephrase the previous question which asked you to speculate on why deaths among vaccinated cases overall is higher while deaths among unvaccinated cases are higher when we split the data into two groups (below 50 and 50 and up). What might be the confounding variable in the relationship between vaccination and deaths?

(write your response here)

Summary

To summarize our findings, let’s begin by calculating the percentages of vaccinated/unvaccinated patients that died. This is essentially the same calculation that we did before, but we’re converting the proportion into a percentage and also doing it all in one code chunk.

delta |>
  count(vaccine, outcome) |>
  group_by(vaccine) |>
  mutate(perc = round(n / sum(n) * 100, 2)) |>
  filter(outcome == "died") |>
  select(-outcome, -n)

# A tibble: 2 × 2
# Groups:   vaccine [2]
  vaccine       perc
  <chr>        <dbl>
1 Unvaccinated  0.17
2 Vaccinated    0.41

Here we do the same thing, but further break down the population by age. We are also asking R to assign the output of this code chunk to a variable called vaccine_age_outcome_perc. The reason for doing this is so that we can do something else with this output later on.

vaccine_age_outcome_perc <- delta |>
  count(vaccine, age, outcome) |>
  group_by(vaccine, age) |>
  mutate(perc = round(n / sum(n) * 100, 2)) |>
  filter(outcome == "died") |>
  select(-outcome, -n)

vaccine_age_outcome_perc

# A tibble: 4 × 3
# Groups:   vaccine, age [4]
  vaccine      age    perc
  <chr>        <chr> <dbl>
1 Unvaccinated 50+    5.96
2 Unvaccinated <50    0.03
3 Vaccinated   50+    1.68
4 Vaccinated   <50    0.02

Lastly, we pivot these data for better display; this just means that we’re reorganizing the output from the previous code into a form that easier to interpret. Notice how we’re using the variable we defined previously in this new code chunk!

vaccine_age_outcome_perc |>
  pivot_wider(names_from = age, values_from = perc)

# A tibble: 2 × 3
# Groups:   vaccine [2]
  vaccine      `50+` `<50`
  <chr>        <dbl> <dbl>
1 Unvaccinated  5.96  0.03
2 Vaccinated    1.68  0.02

Weighting

We now know that it’s misleading to talk about a single death rate for an unvaccinated population since age is a confounding variable. However, one thing we can do is to combine the two rates for the two age groups in a way that accounts for the sizes of those two groups.

First, calculate what proportion of the total population is in each of our two age categories.

age_props <- delta |>
  count(age) |>
  mutate(p = n / sum(n))

age_props

# A tibble: 2 × 3
  age        n     p
  <chr>  <int> <dbl>
1 50+    30747 0.115
2 <50   237419 0.885

Question 10

Summarize in 1-2 sentences the results of this calculation.

(add your response here)

Next, we combine our two death rates to account for age using these proportions.

vaccine_age_outcome_perc |>
  mutate(perc_wt = if_else(age == "50+", perc * 0.115, perc * 0.885)) |>
  group_by(vaccine) |>
  summarize(perc = sum(perc_wt))

# A tibble: 2 × 2
  vaccine       perc
  <chr>        <dbl>
1 Unvaccinated 0.712
2 Vaccinated   0.211

Question 11

Summarize in 1-2 sentences the results shown in this table.

(add your response here)

Question 12

Revisiting the question we posed to start with: How do deaths from COVID cases compare between vaccinated and unvaccinated?

(add your response here)

Acknowledgements

This case study is inspired by Statistical Literacy: Simpson’s Paradox and Covid Deaths by Milo Schield.