Two Sided Tests
Chapter 14
Case Study: opportunity cost
Will a prompt about saving money for future purchases would lead students to spend less?
\(H_0\) Null hypothesis Reminding students that they can save money for later purchases will not have any impact on spending decisions.
\(H_A\) Alternatve hypothesis Reminding students that they can save money for later purchases will reduce the chance they will continue w/ purchase.
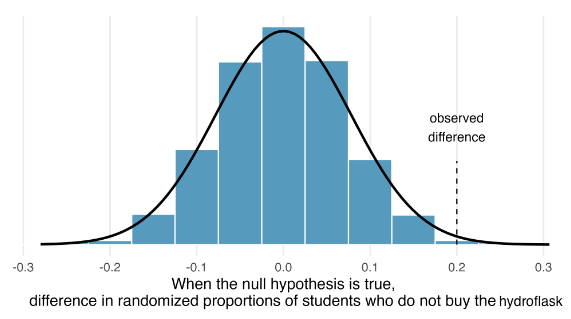
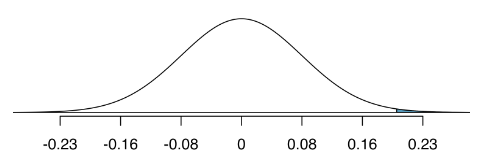
p-value
probability of observing difference of 0.2 or larger (more extreme)
Alternative Alternatives
\(H_A\) Alternatve hypothesis Reminding students that they can save money for later purchases will reduce the chance they will continue w/ purchase.
But why is this the alternative hypothesis? Couldn’t we also imagine that the prompt would increase the chance that students buy the item?
- Probably not
- And that’s not the research question!
Danger of One-Sided Hypotheses
- Framing \(H_A\) to match the data elevates risk of Type I error.
- Framing \(H_A\) to match what we think elevates risk of confirmation bias
Two-Sided Test
Research question: does administering blood thinning medication have an impact on survival rate of patients that have undergone CPR?
\(H_0\) Null hypothesis Blood thinners do not have an effect on survival rates.
\(H_A\) Alternatve hypothesis Blood thinners do have an impact on survival rates.
Data
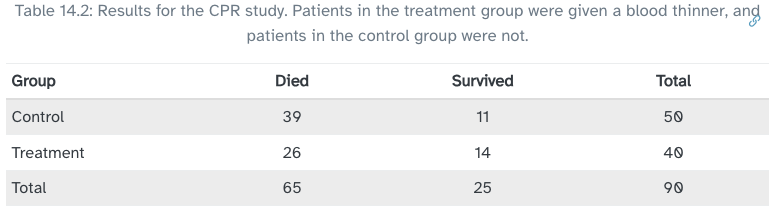
Difference in proportions: \[ \hat{p_T} - \hat{p_C} = \frac{14}{40} - \frac{11}{50} = 0.13 \]
Randomized null distribution
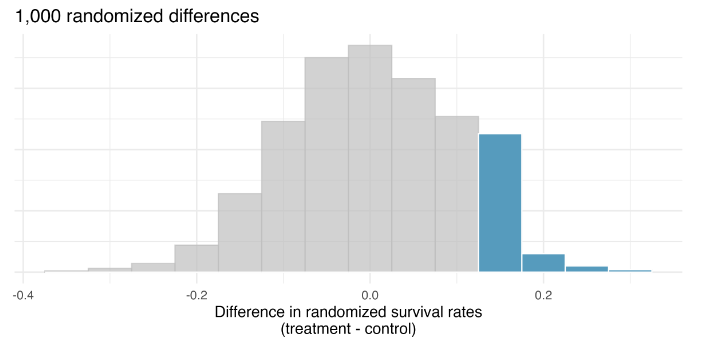 Observations that are at least as large as 0.13
Observations that are at least as large as 0.13
Randomized null distribution
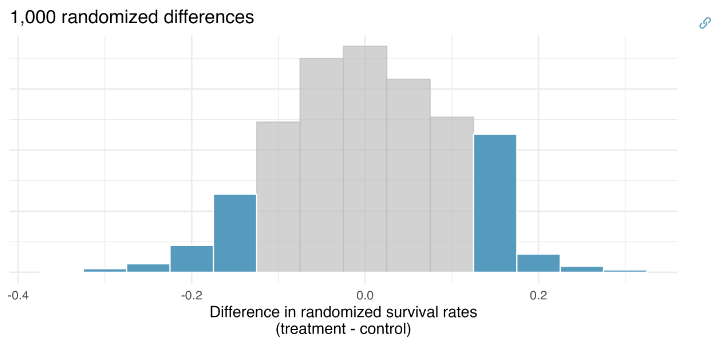 Observations that are at least as extreme as \(\pm 0.13\), in either direction!
Observations that are at least as extreme as \(\pm 0.13\), in either direction!
Two-sided tests
p-value for two-sided test
First find p-value for one tail and then double it!
Default to two-sided test
Only use a one-sided hypothesis test if you have a reason to focus on one direction in the alternative