Inference with mathematical models
Chapter 13
Welcome Back!
- New Groups
- Feedback
- Big Picture
- Chapter 13
New Groups
- Introductions + check-in with everyone
- Remember to respect different ways of engaging with class!
Feedback from mid-semester survey
- More stats, less coding?
- More frequent check-ins?
- Remember that handing in the labs is only the first step – revise and resubmit!
Semester at a glance
Weeks 1-7
- Basics of R and posit.cloud (a big lift – high five!!)
- General concepts: variables, graphs, linear models, p-value, null/alternative hypothesis, confidence intervals
Weeks 8-14
- Statistical Inference (review p-value, hypothesis tests, confidence interval)
Inference with mathematical models
Describe the shape …
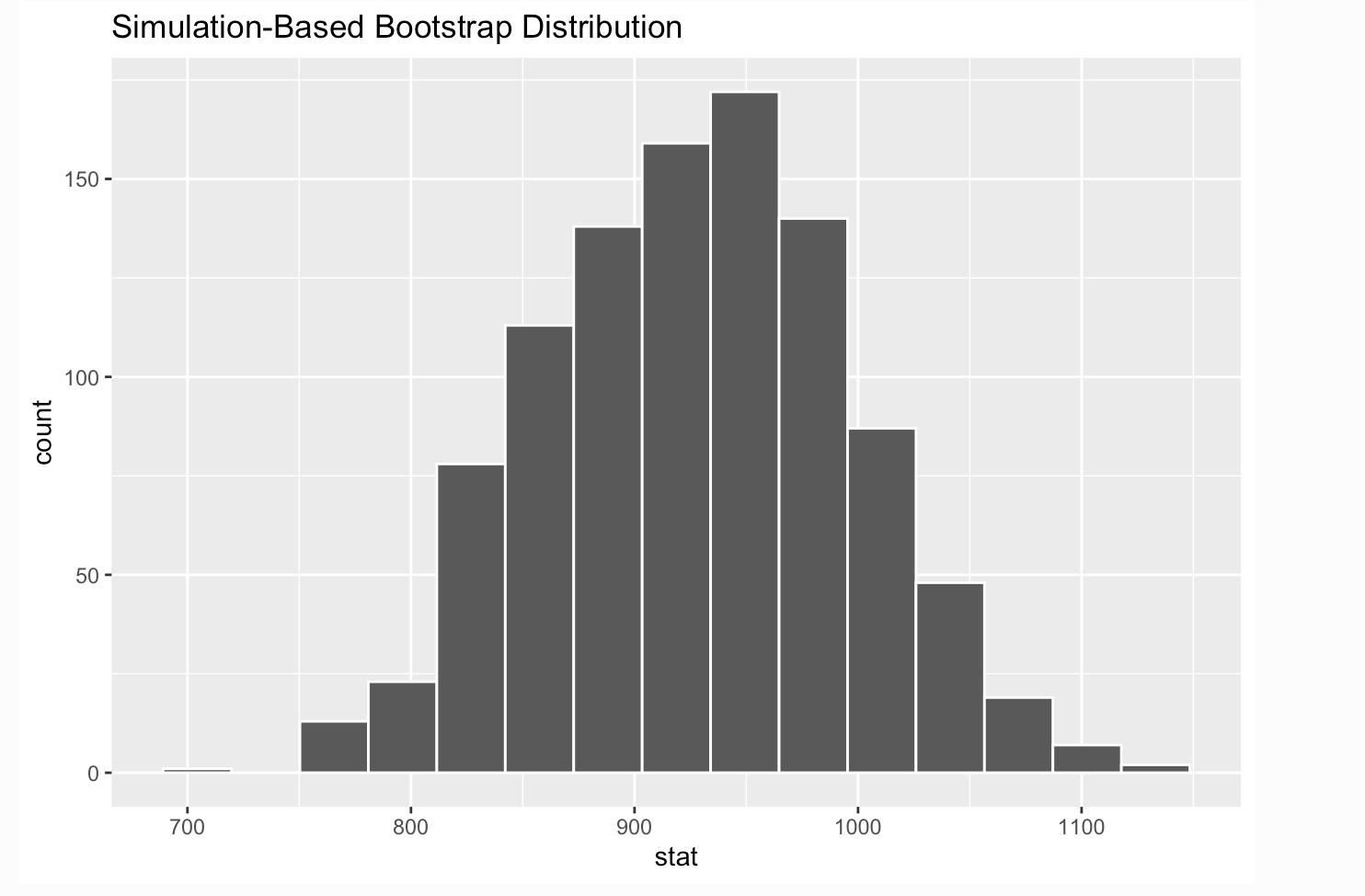
Lemurs mean weight sampling distribution (AE 07)
Describe the shape …
Transplant sampling distribution (Ch. 12)
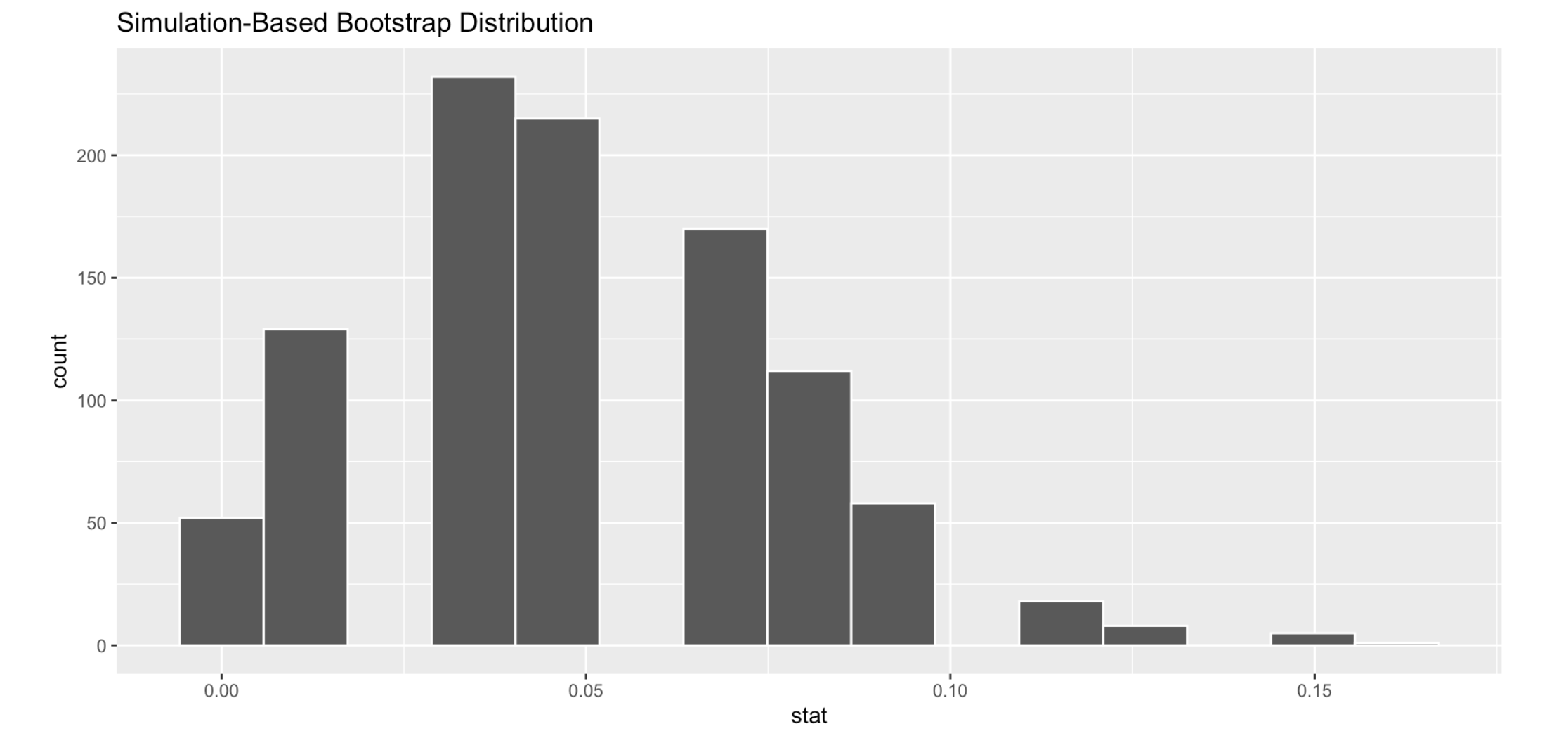
Describe the shape …
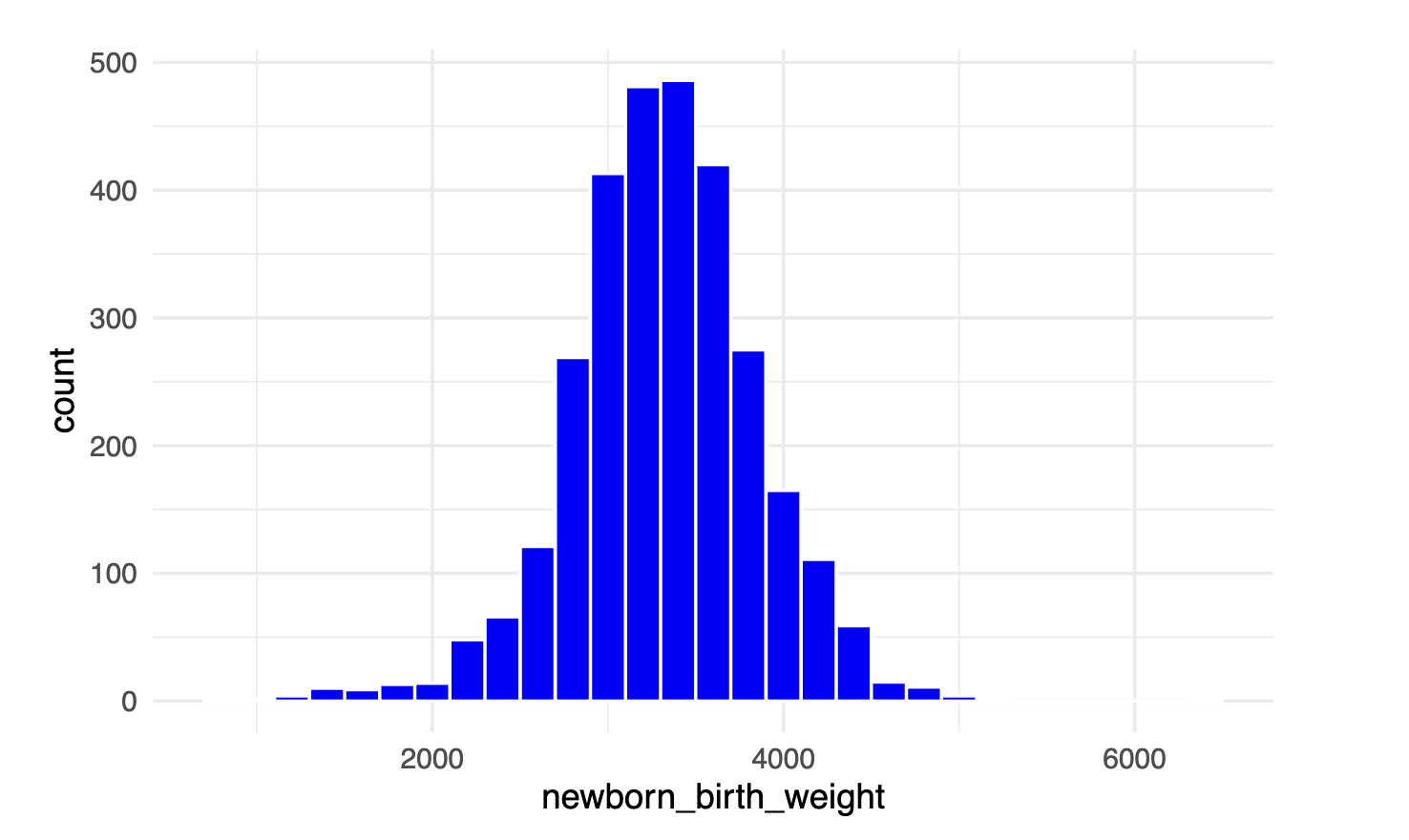
newborn birth weight
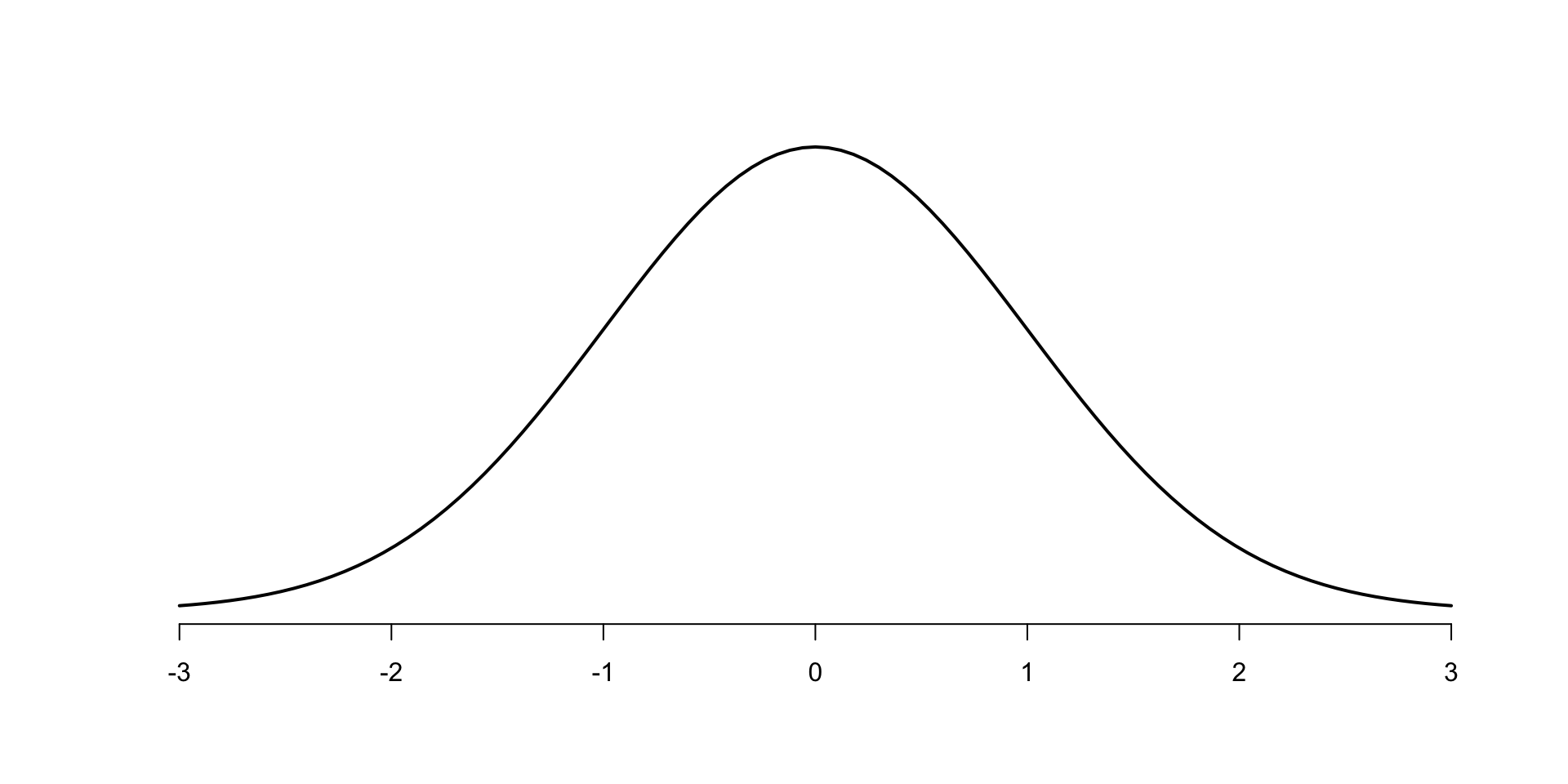
Normal distribution
- aka bell curve or Gaussian curve
- “normal” has a specific, technical meaning
Central Limit Theorem (CLT)
If certain conditions are met then the distribution of any sample statistic is normal.
tl;dr
Normal distributions are very common - we should take a closer look!
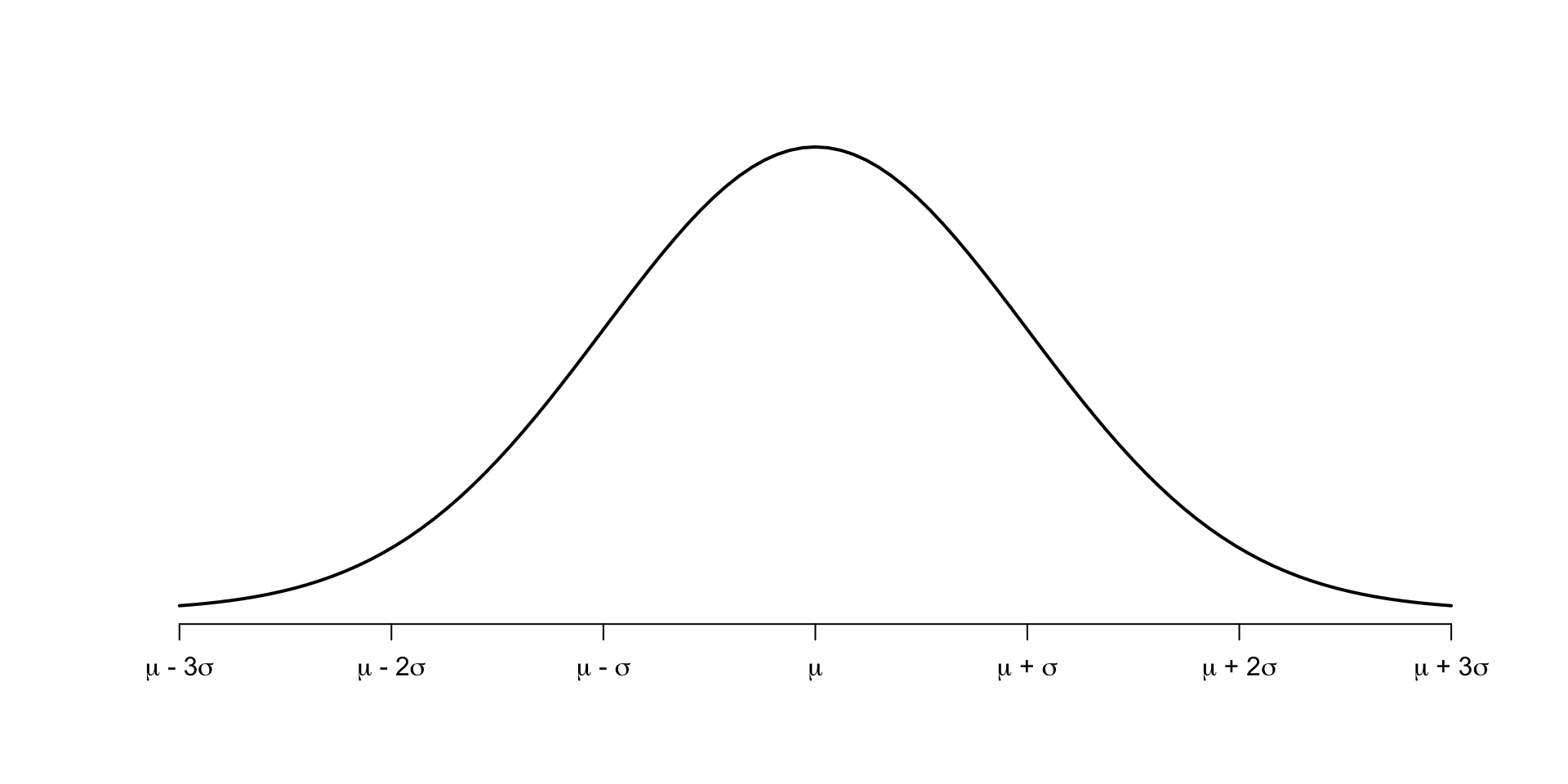
Normal distribution N(\(\mu\), \(\sigma\))
- centered at mean (\(\mu\))
- width characterized by standard deviation (\(\sigma\))
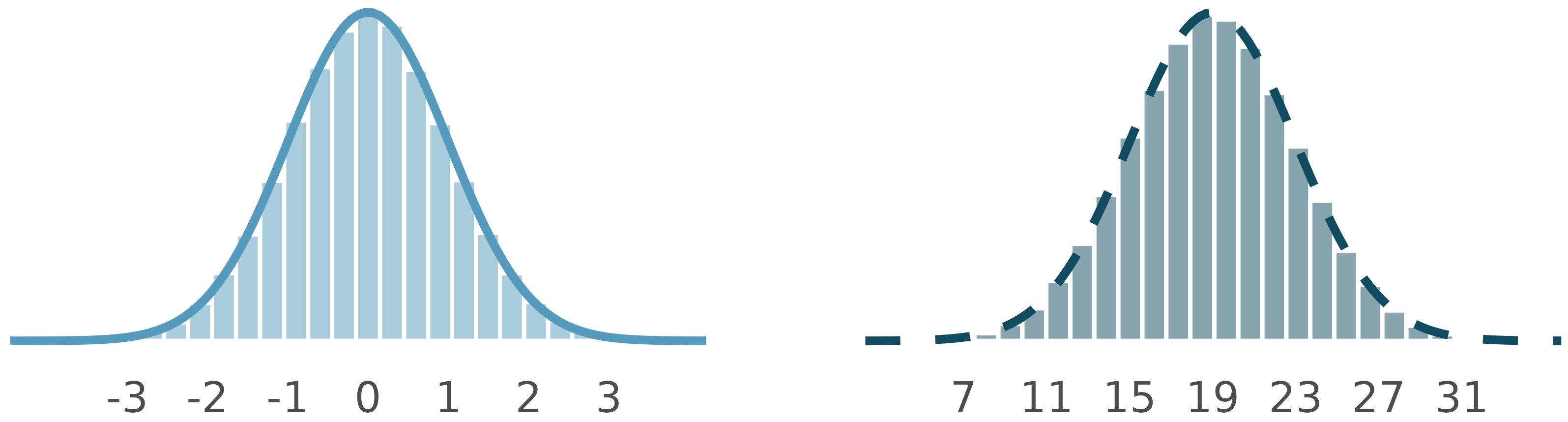
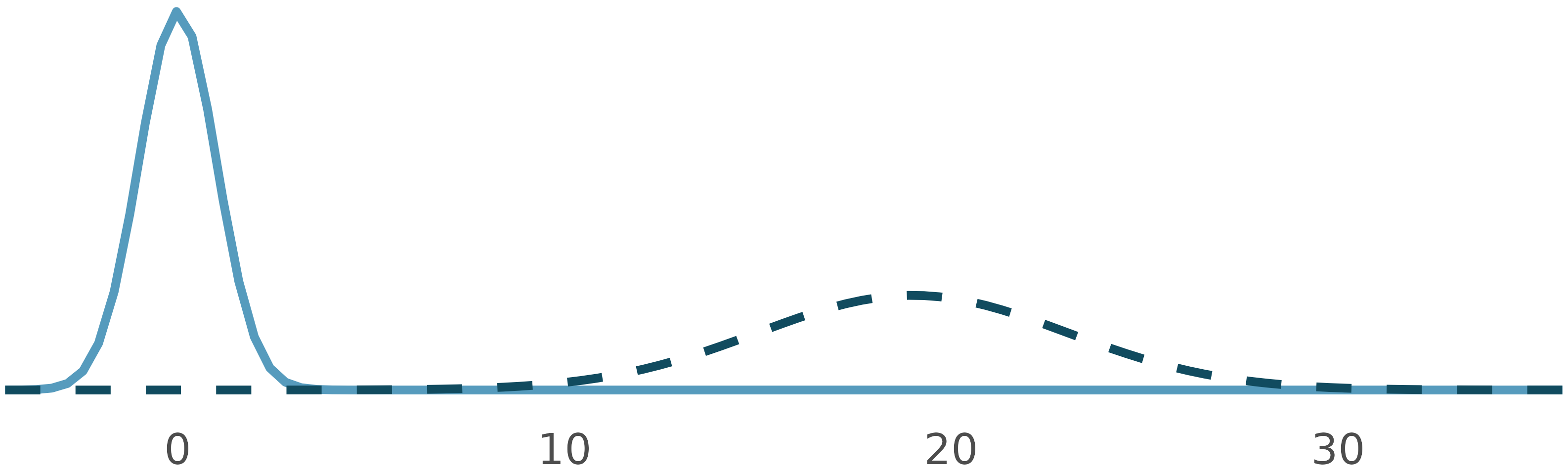
Normal distributions
How are these normal distributions similar? How are they different? Which one is \(N(\mu = 0, \sigma = 1)\) and which \(N(\mu = 19, \sigma = 4)\)?
Comparing Distributions
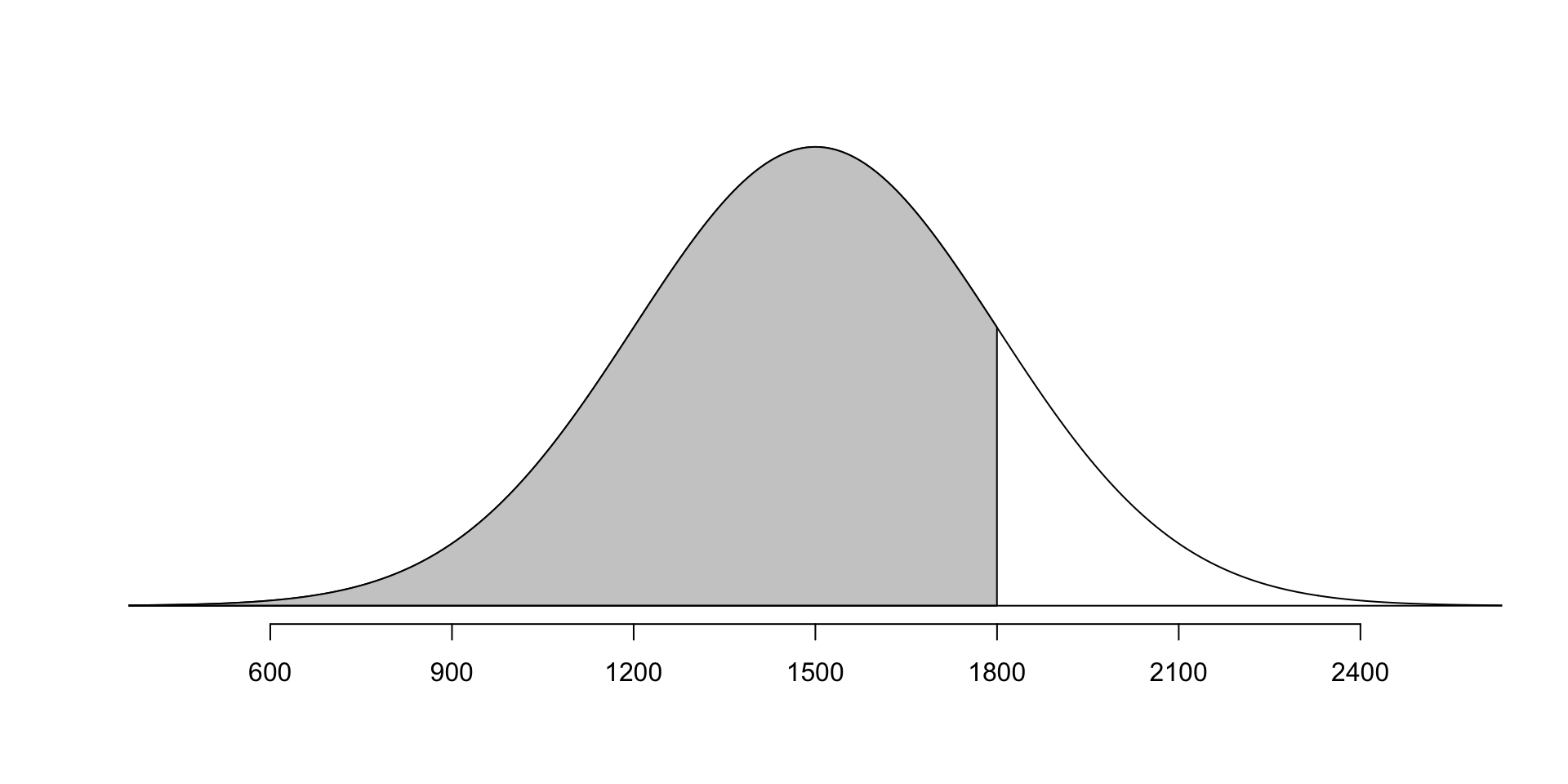
SAT scores follow a nearly normal distribution with a mean of 1500 points and a standard deviation of 300 points. ACT scores also follow a nearly normal distribution with mean of 21 points and a standard deviation of 5 points.
Suppose Nel scored 1800 points on their SAT and Sian scored 24 points on their ACT. Who performed better?
Compare Graphs
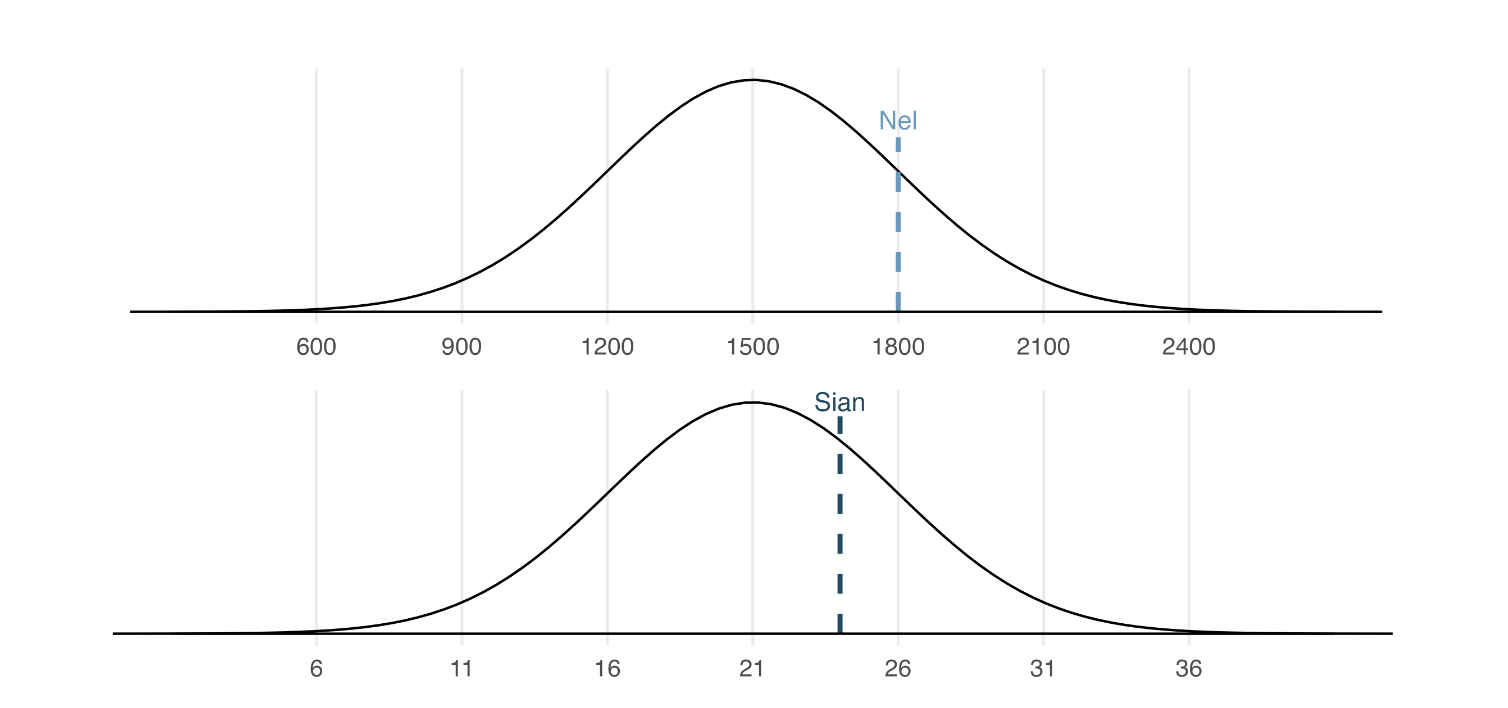
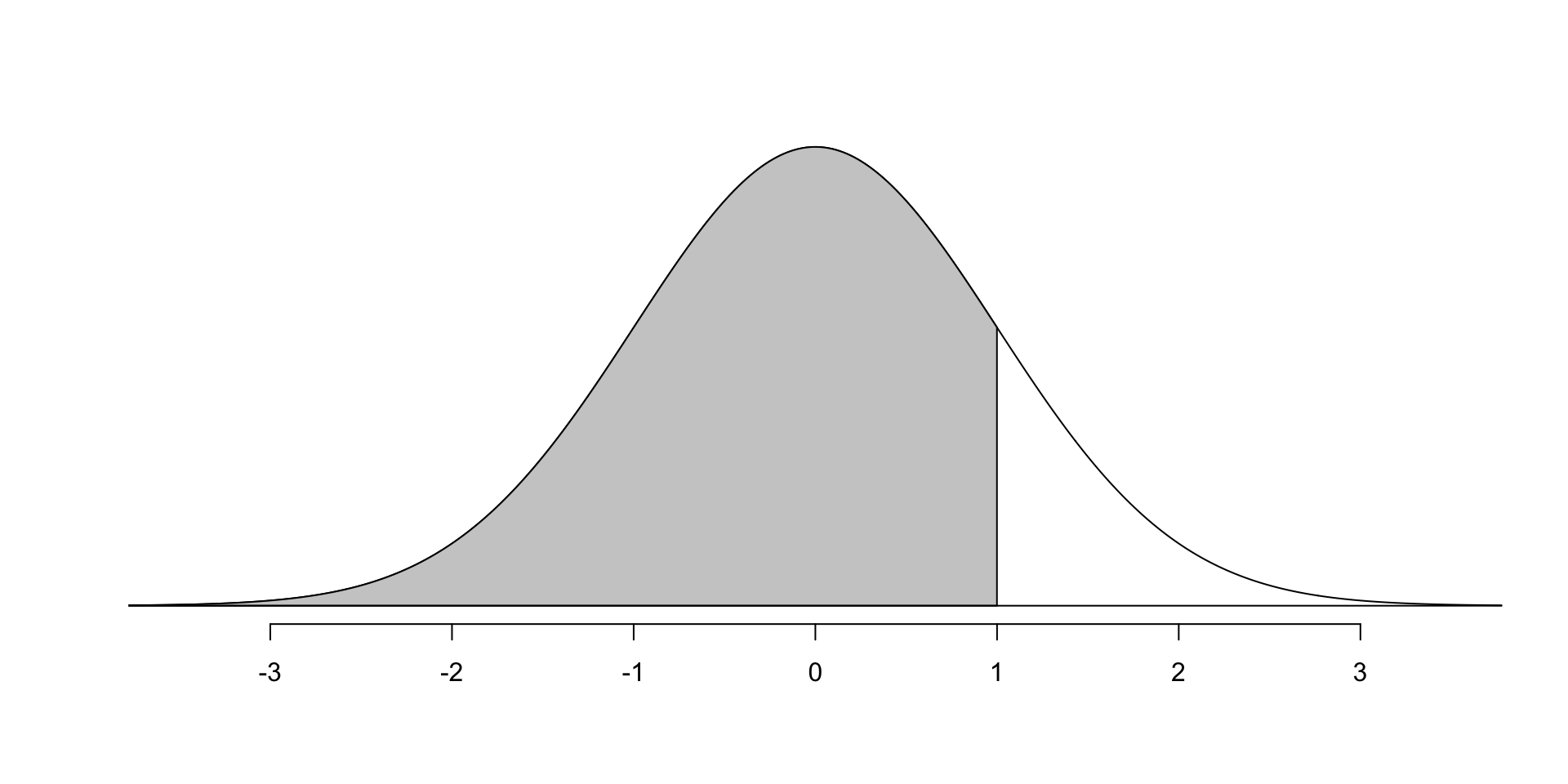
- Nel is 1 sd from mean
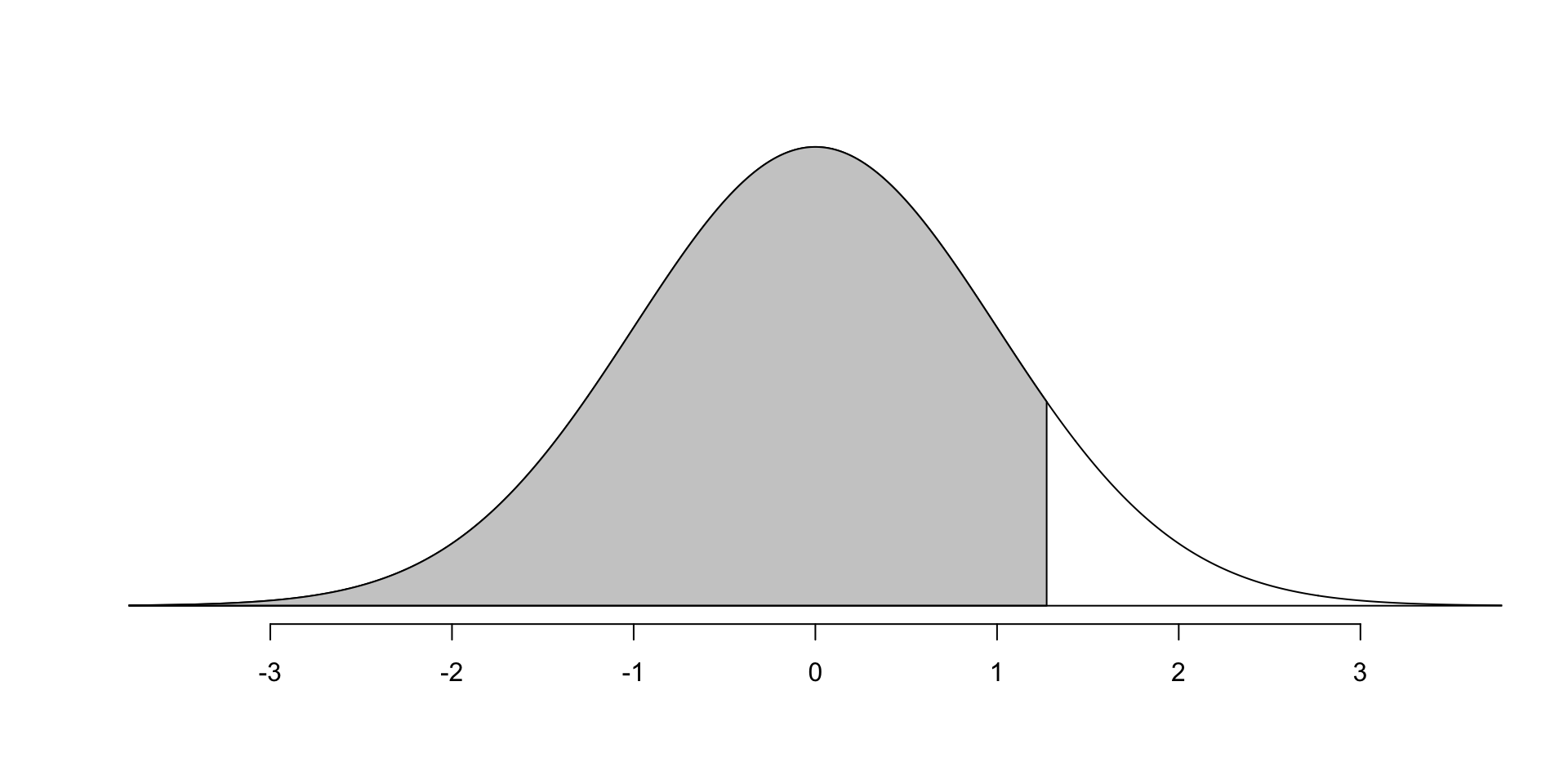
- Sian is less than 1 sd from mean
Compare Z-Scores
Z-score measures how many standard deviations from the mean an observation is:
\[ Z = \frac{ x - \mu}{\sigma} \]
- Nel: \(Z = \frac{ 1800 - 1500}{300} = 1\)
- Sian: \(Z = \frac{ 24 - 21}{5} = 0.6\)
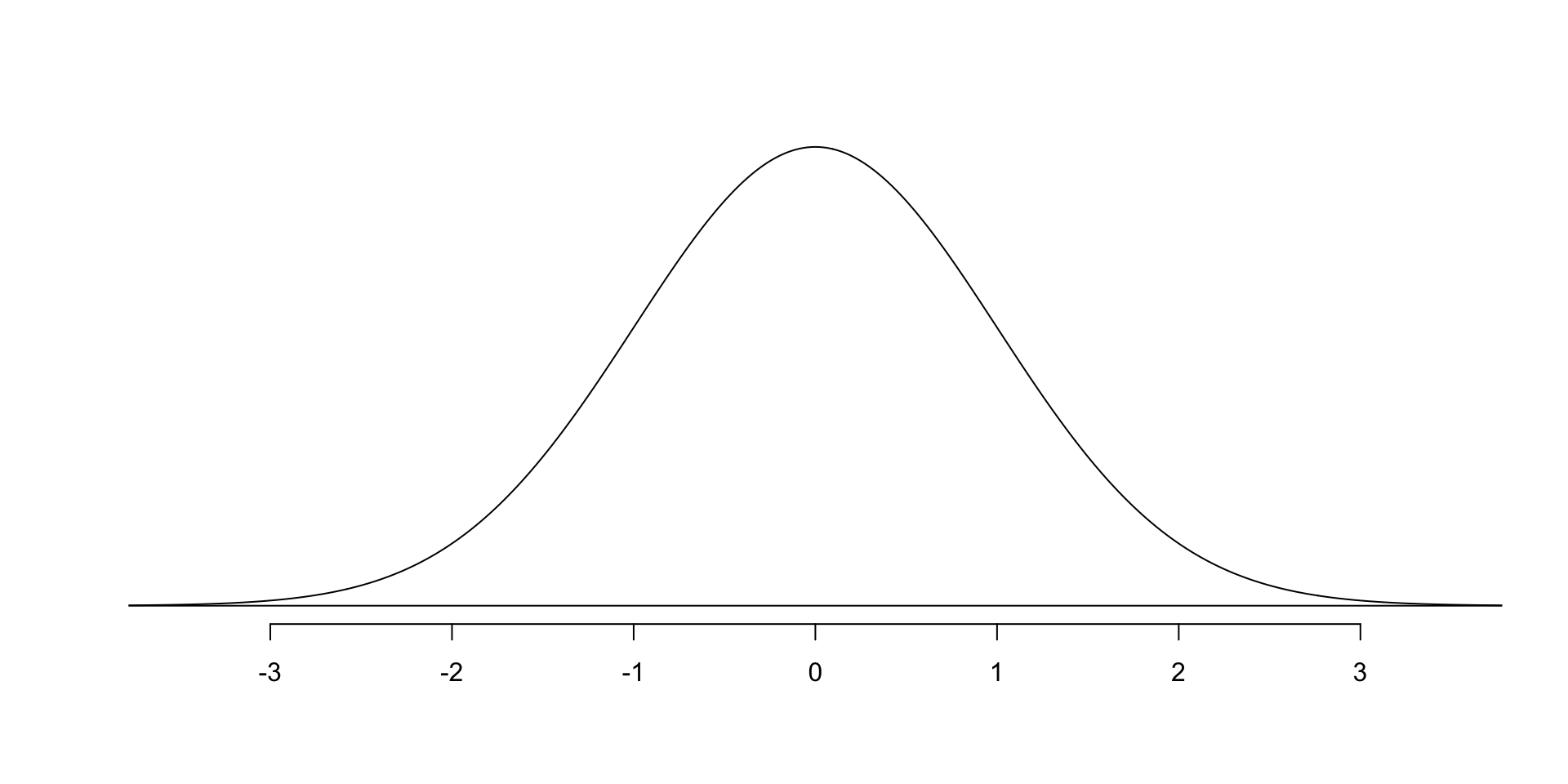
Standard Normal Distribuion
- mean is 0
- standard deviation is 1
- area under curve is 1
Z-scores also tell us about percentiles.
Nel had SAT score 1800 corresponding to \(Z=1\). What percentile are they in?
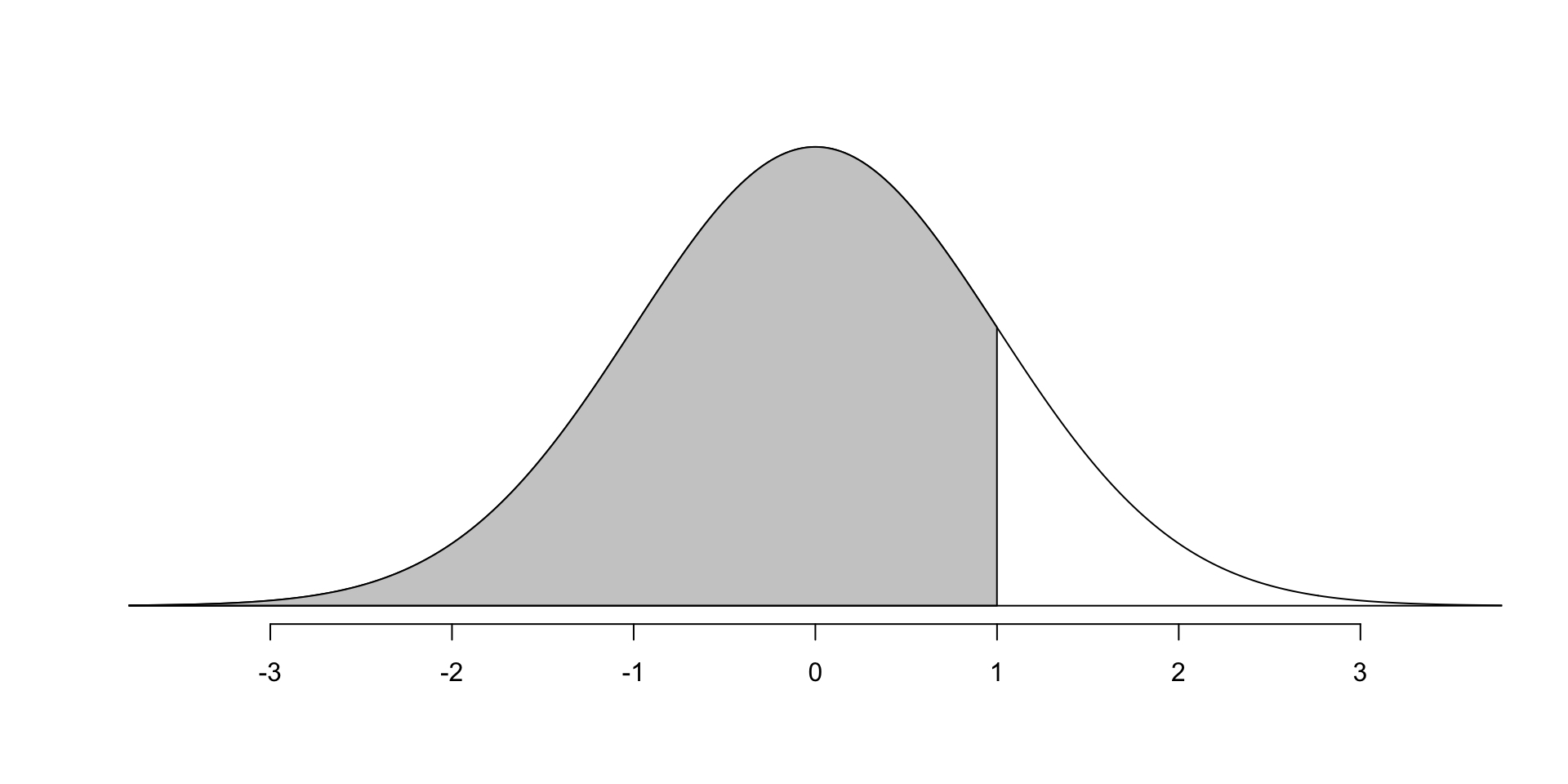
What percentage of scores are less than 1800? Same as shaded area!
Find the shaded area
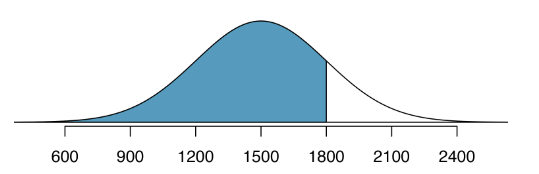
- Use a table (need z-score)
- Use technology (dont need z-score)
Z-score table
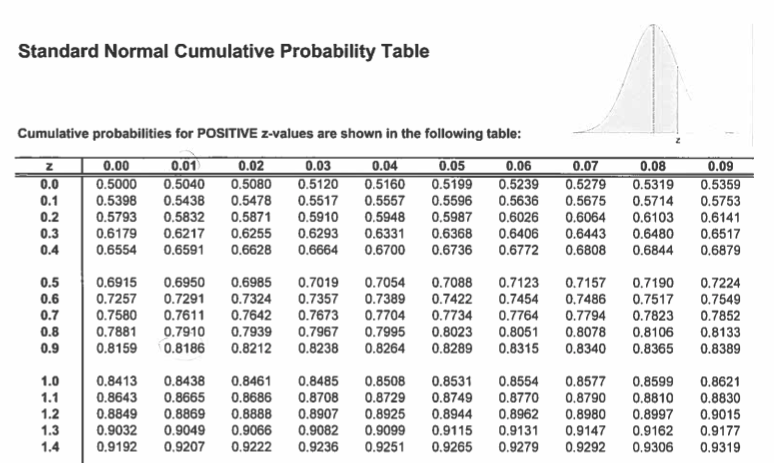
A z-score of 1 corresponds to 84th percentile.
Z-score to percentile with technology
aka Normal Cumulative Probability (CDF)
Other tech tools
Technology without Z-score
Percentile to Z-score
What z-score would correspond to 90th percentile?
Percentile to Z-score with table
What z-score would correspond to 90th percentile?