Linear Regression, Cont.
Chapter 7
In groups
- Discuss Homework: 7.5 #7, 21, 30, 31
Goals
- Interpreting \(r\) (correlation coefficient)
- Interpreting linear model
Correlation Coefficient
A number between -1 and 1 which describes the strength and direction of a linear relationship. Denoted \(r\)
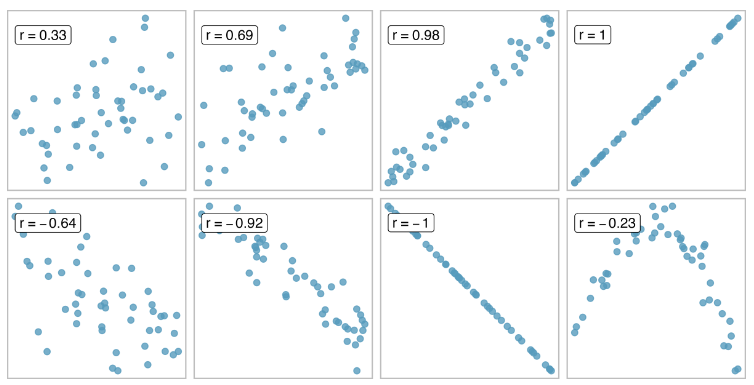
What do these datasets all have in common?
The all have roughly the same correlation \(r = -0.06\)
Correlation is only meaningful for linear assocations
Strength of Fit
Correlation \(r\) describes strength and direction of linear relationships
more commonly use \(r^2\) – which is usually capitalized \(R^2\).
\(R^2\) measures the amount of variation in outcome variable that’s explained by the linear model.
\(R^2\) Example
For our cricket chirps we found \(r=0.825\)
so \(R^2 = (0.825)^2 = 0.681\).
This means that \(0.681\) or \(68.1\)% of the variation we see in cricket chirp rates can be explained by the ambient temperature. What might account for the other \(31.9\)% of the variation in chirps?
Linear Regression
\[ \hat{y} = b_0 + b_1 \cdot \hat{x} \]
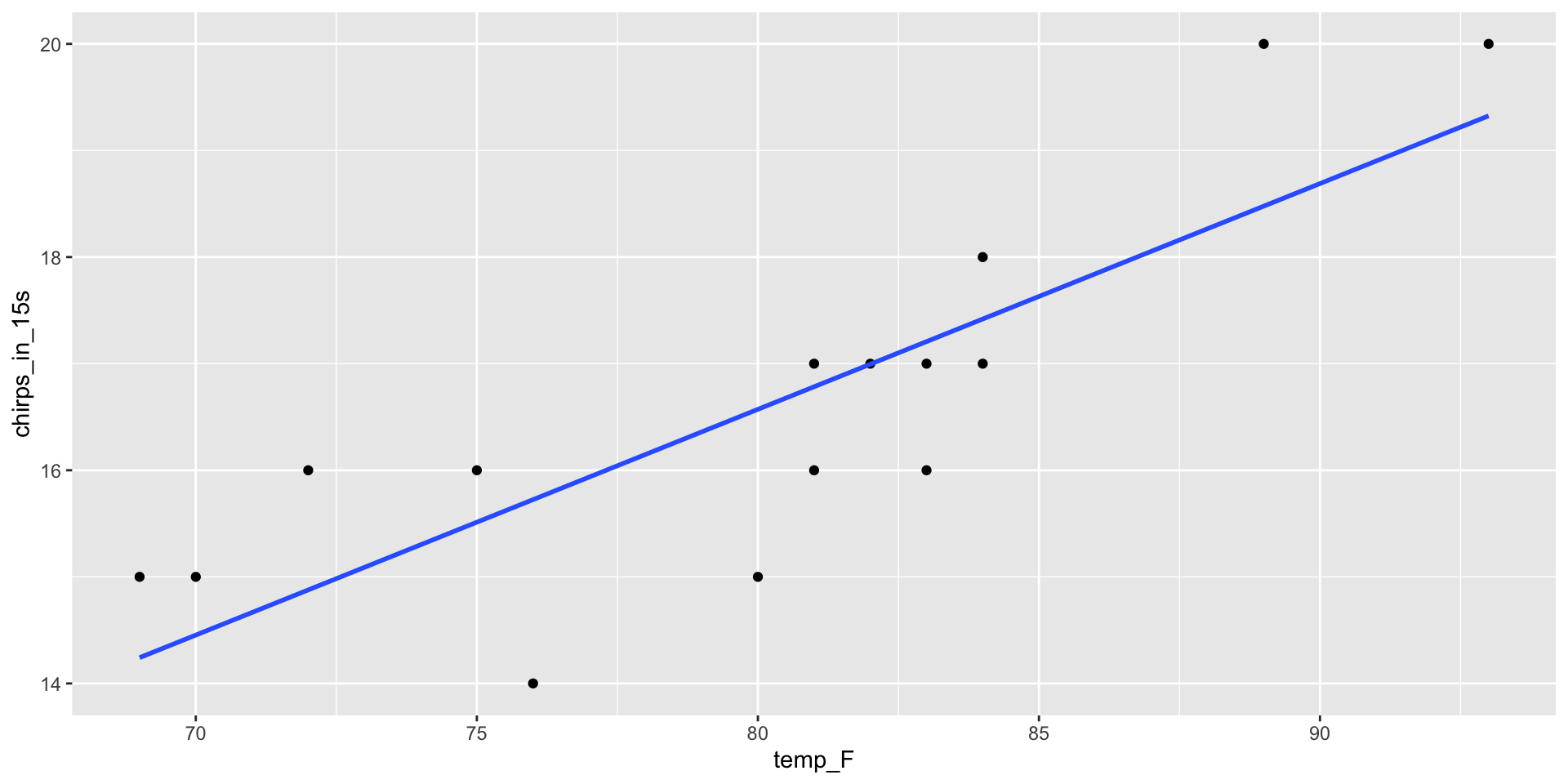
A Shortcut!
# A tibble: 2 × 5
term estimate std.error statistic p.value
<chr> <dbl> <dbl> <dbl> <dbl>
1 (Intercept) -0.372 3.23 -0.115 0.910
2 temp_F 0.212 0.0402 5.27 0.000151\[ \hat{y} = -0.372 + 0.212 \, \hat{x} \]
Don’t Extrapolate!!
\[ \hat{y} = -0.372 + 0.212 \, \hat{x} \]
What do you expect the chirp rate will be if temperature is 100?
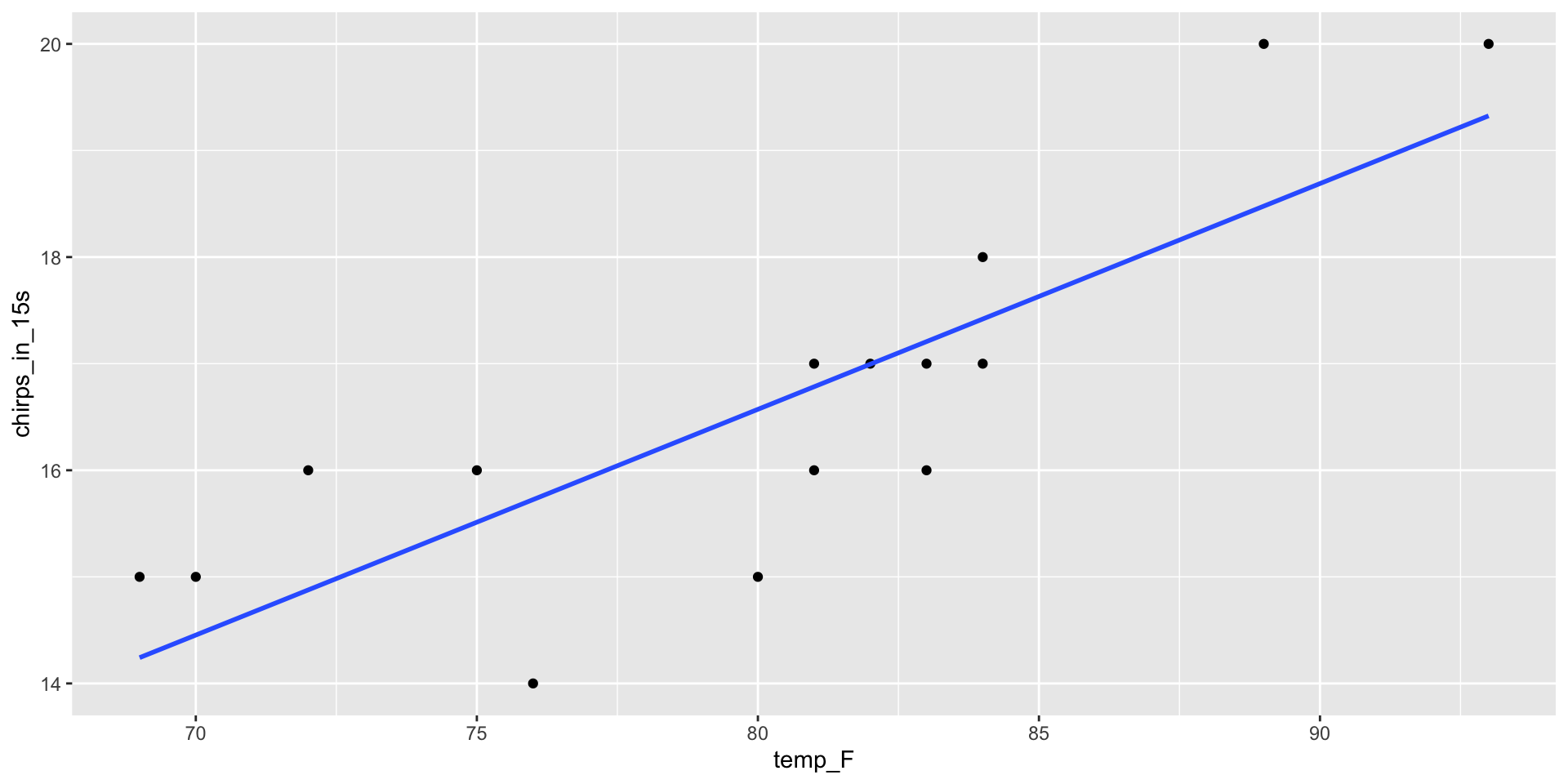
Interpreting the slope
\[ \hat{y} = -0.372 + 0.212 \, \hat{x} \]
Slope of \(0.212\) means that for every increase of 1 degree (F), the chirp rate will increase by 0.212.
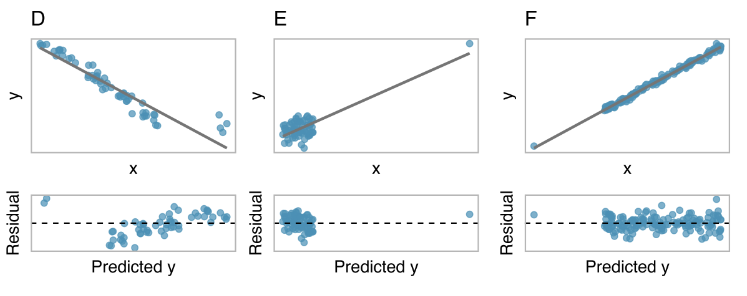
Outliers
Each data set has at least one outlier. How do the outliers affect the slope of the regression line?
Practice for next time
Section 11.5 #1, 3
Now head to Posit Cloud for AE05 - Finnish Fish!