Linear Regression

Chp 7

In groups

• Discuss Homework: 7.5 #1, 3, 7, 9, 19

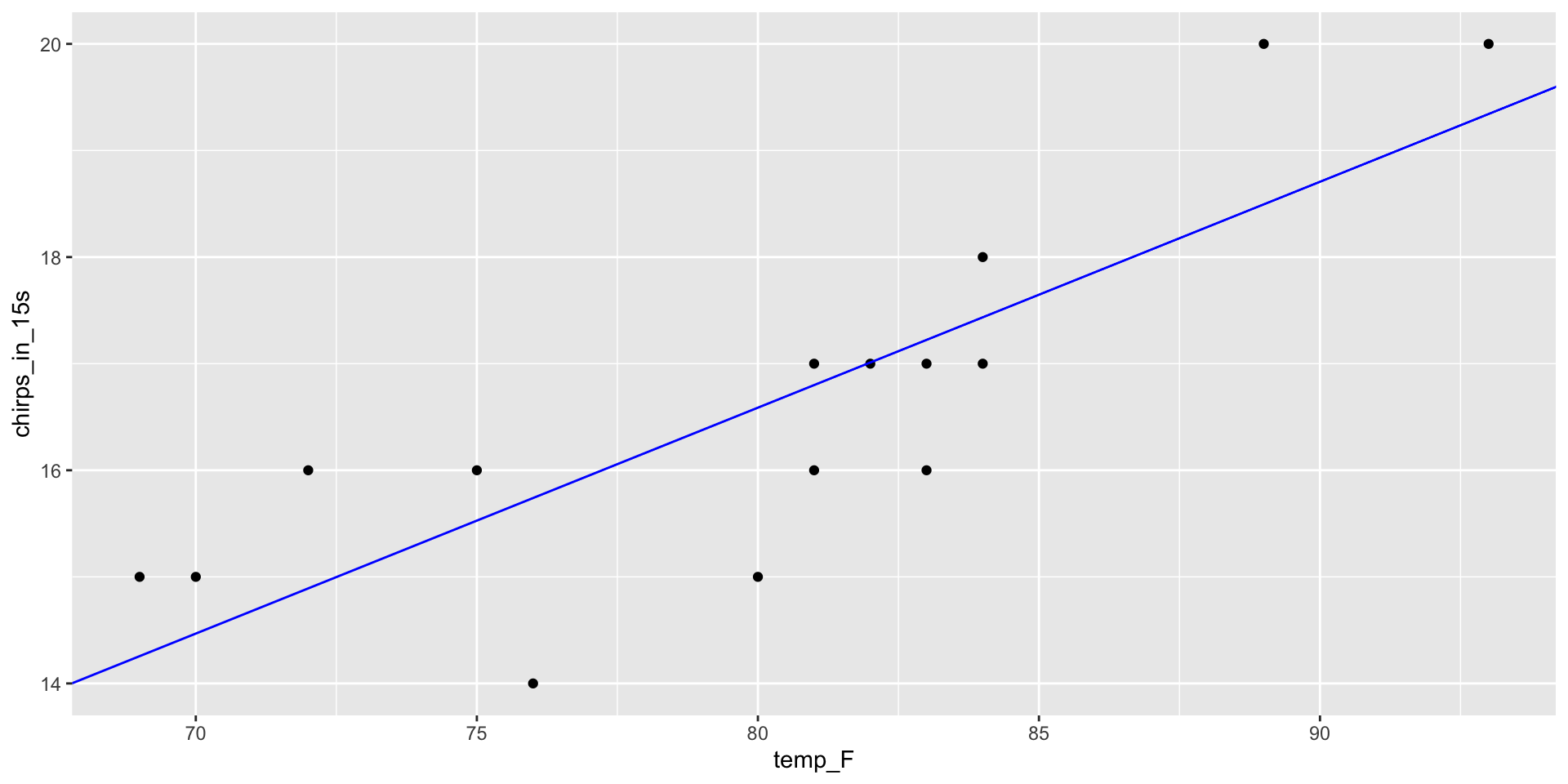
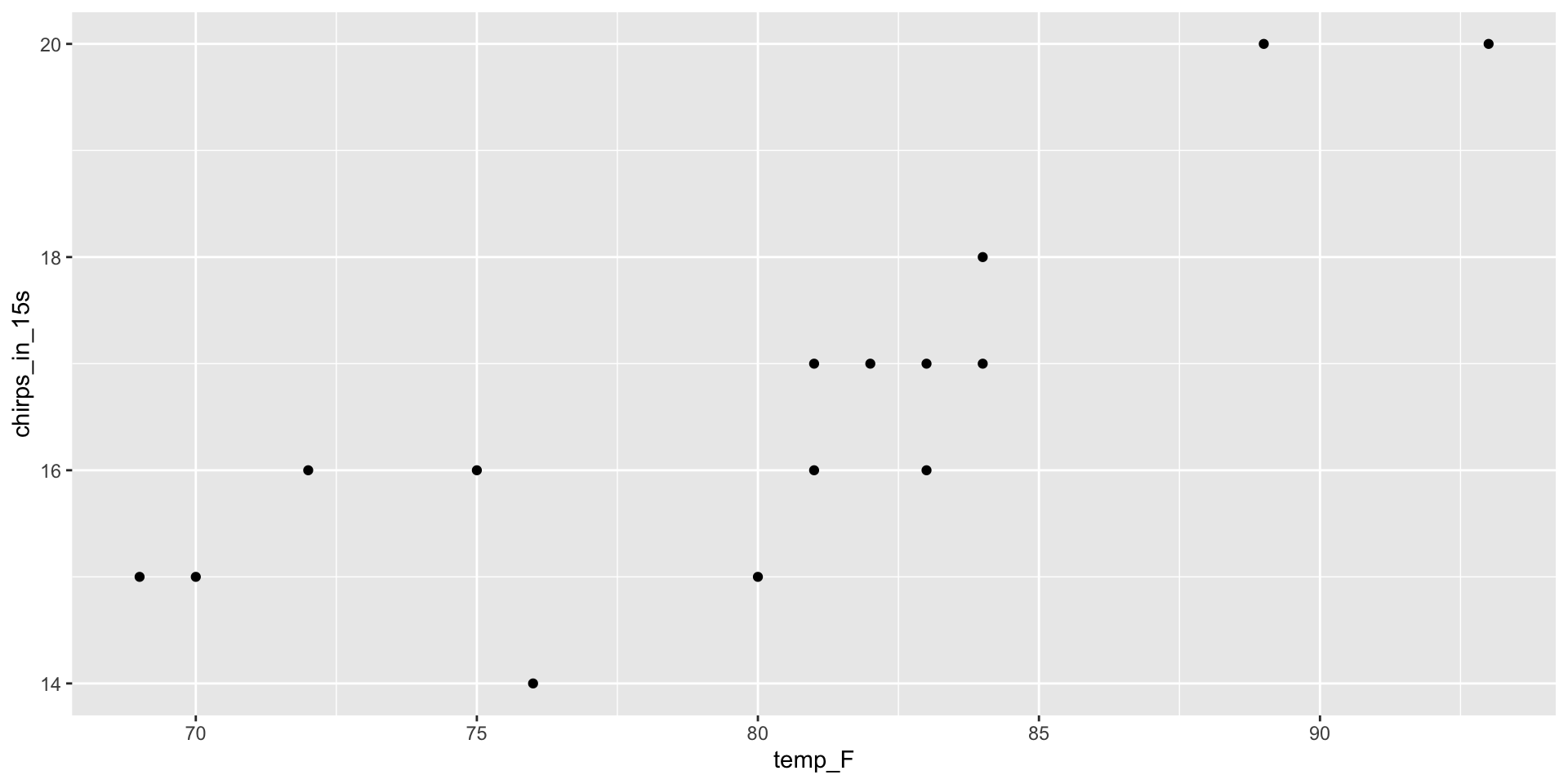
Cricket Chirps and Temperature

Do cricket chirp rates and air temperature seem to be associated?

Linear Regression

Best fit line

Linear model

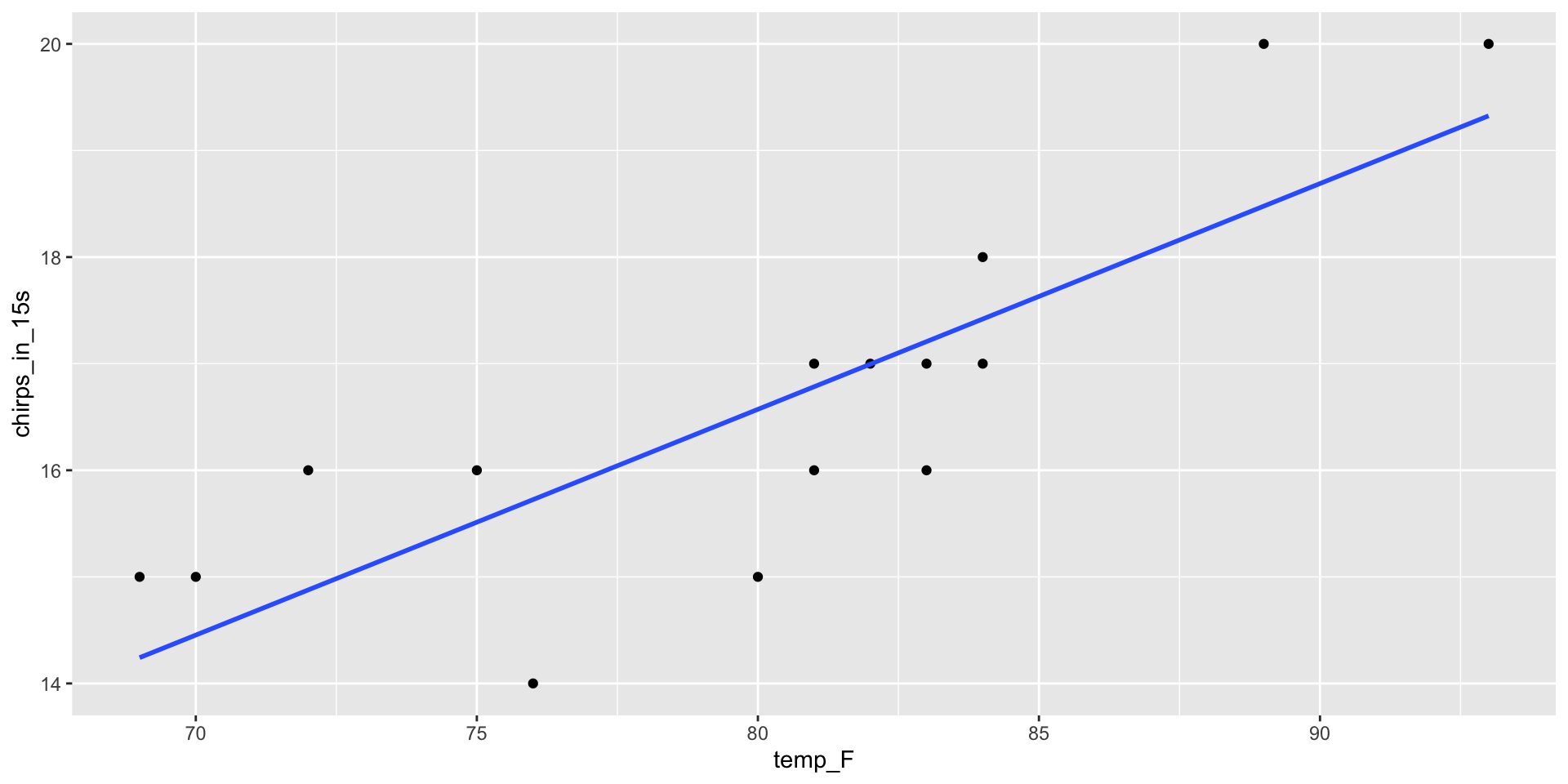
Finding the regression line

Recall – a line has the equation \[ y = m x + b\] where \(m\) is the slope and \(b\) is the intercept.

• \(x\) is the predictor or explanatory or independent variable

• \(y\) is the response or outcome or dependent variable. In prediction problems, this is what we are interested in predicting.

Residuals

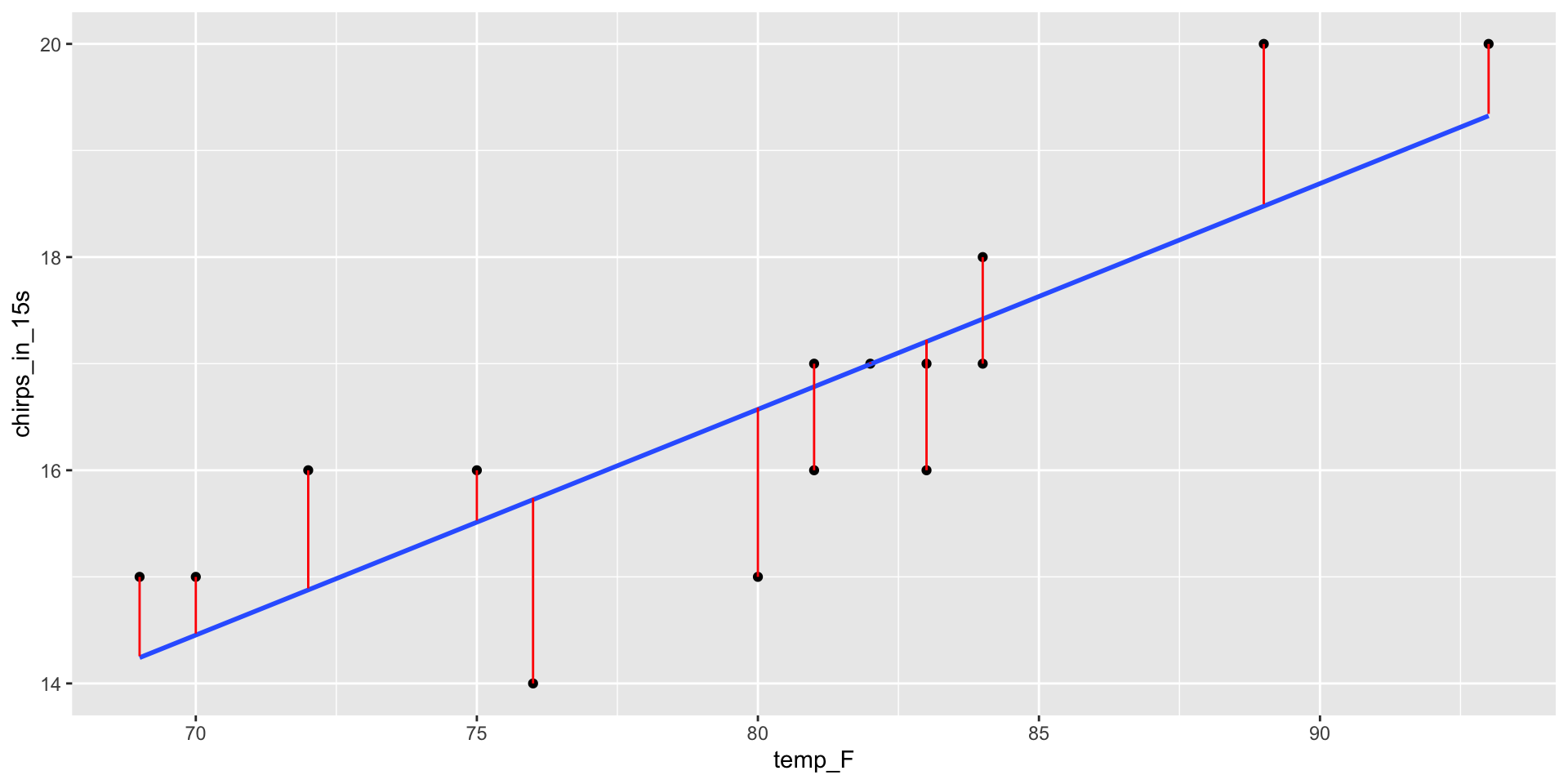
least squares regression line

\[ \hat{y} = b_0 + b_1 \cdot \hat{x} \]

• Minimizes (sum of squared) distance between data points and line
• Residuals balance out above and below line
• The point \((\bar{x}, \bar{y})\) always lies on line (though it’s not necessarily a data point!)

Correlation coefficient, r

Also called the Pearson Product-Moment Correlation, here’s how r is calculated:

\[ r = \frac{1}{n-1}\sum_{i=1}^n \frac{ x_i - \bar{x}}{s_x} \frac{y_i - \bar{y}}{s_y} \] We’ll have R do this for us!

Correlation coefficient, r

crickets |>
  summarize(N = n(), 
            mean_x = mean(temp_F),
            sd_x = sd(temp_F),
            mean_y = mean(chirps_in_15s),
            sd_y = sd(chirps_in_15s),
            r = cor(temp_F, chirps_in_15s)
  )

# A tibble: 1 × 6
      N mean_x  sd_x mean_y  sd_y     r
  <int>  <dbl> <dbl>  <dbl> <dbl> <dbl>
1    15   80.1  6.72   16.6  1.72 0.825

Finding the regression line

\[ \hat{y} = b_0 + b_1 \cdot \hat{x} \] First we find the slope: \[b_1 = r \left( \frac{s_y}{s_x} \right)\]

In this formula:

• \(r\) = correlation coefficient
• \(s_y\) = standard deviation of \(y\)
• \(s_x\) = standard deviation of \(x\)

Finding the regression line

\[ \hat{y} = b_0 + b_1 \cdot \hat{x} \] Next we use the fact that \((\bar{x}, \bar{y})\) is on the line. Plug these values into line equation

\[\bar{y} = b_0 + b_1 \cdot \bar{x} \] Now everything is known except \(b_0\) so we can solve for that!

\[ b_0 = \bar{y} - b_1 \bar{x} \]

Calculuate!

lm(chirps_in_15s ~ temp_F, data=crickets)

Call:
lm(formula = chirps_in_15s ~ temp_F, data = crickets)

Coefficients:
(Intercept)       temp_F  
    -0.3721       0.2118  

Linear Model

\[ \hat{y} = 0.212 \hat{x} - 0.372 \]

ggplot(data = crickets, aes(x = temp_F, y = chirps_in_15s)) +
  geom_point() +
  geom_abline(slope = 0.212, intercept = -0.372, color="blue")

Next Steps

• What can we do with our linear model (i.e. regression line)?
• What is the significance of correlation coefficient \(r\)?