Hypothesis Testing with Randomization, part two

Chapter 11

In groups

  • Discuss Homework: Chapter 11, #3, 5, 7

Gender Discrimination Study

On Tuesday we looked at a study on gender discrimination. The study observed that \(87.5\%\) of male candidates were promoted whereas \(58.3\%\) of female candidates were promoted.


# A tibble: 4 × 4
# Groups:   gender [2]
  gender decision         n  prop
  <fct>  <fct>        <int> <dbl>
1 male   promoted        21 0.875
2 male   not promoted     3 0.125
3 female promoted        14 0.583
4 female not promoted    10 0.417


Difference in proportions: \(0.583 - 0.875 = -0.292\)

Test Statistic

diff_orig <- gender_discrimination |>
  group_by(gender) |>
  summarize(prop_promoted = mean(decision == "promoted")) |>
  summarize(stat = diff(prop_promoted))

# see the result
diff_orig
# A tibble: 1 × 1
    stat
   <dbl>
1 -0.292

State the Hypotheses

  • \(H_0\) there is no difference between the two groups. Men and women are promoted at the same rate.

  • \(H_A\) there is a difference. Men are promoted more often than women.


The study observed a difference of \(-0.292\). How unusual would this be if the null hypothesis is true?


If it’s very unusual then we have evidence to reject \(H_0\)

Simulation

  • Randomly shuffle a deck of 48 cards that has 35 “promoted” and 13 “not promoted”
  • Deal into two groups
  • Calculate new difference in proportions
  • Repeat!
  • Look at the distribution of simulation results

Simulation with R using infer package

set.seed(1234)

gender_discrimination_perm <- gender_discrimination |>
  specify(decision ~ gender, success = "promoted") |>
  hypothesize(null = "independence") |>
  generate(reps = 1000, type = "permute") |>
  calculate(stat = "diff in props", order = c("male", "female"))

  • specify – what variables are we looking at?

  • hypothesize – what kind of hypothesis test are we doing?

  • generate – do a simulation (many times)

  • calculate – results of the simulation

Visualize results

gender_discrimination_perm |>
  visualize(bins=30) +
  shade_p_value(obs_stat = diff_orig, direction = "less")

p-value

probability of observing data as (or more) extreme than what we actually got, assuming the null hypothesis is true


In our example, we would want to know how many of the simulated differences were less than or equal to \(-0.29\)

gender_discrimination_perm |>
  filter( stat <= -0.29 ) |>
  nrow()
[1] 26


In other words, our observed value of \(-0.29\) happened in the simulations 26 times, or w/ probability \(26/1000 = 0.026\)

Compute p-value with R

gender_discrimination_perm |>
  get_p_value(obs_stat = diff_orig, direction = "less")
# A tibble: 1 × 1
  p_value
    <dbl>
1   0.026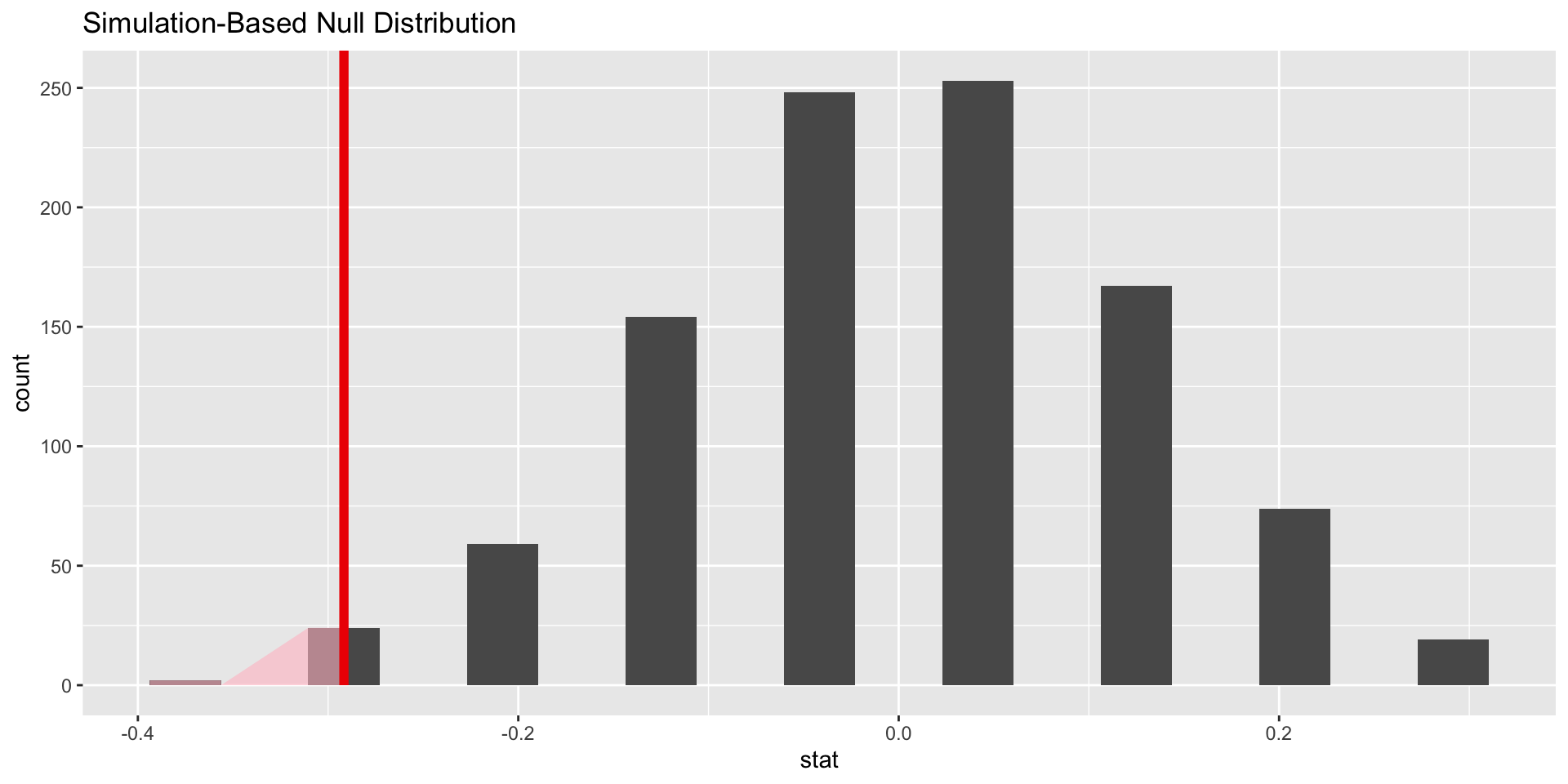

Discernability Level

  • How much evidence do we require to reject \(H_0\)?

  • How skeptical are we?

  • What threshold should we compare p-value to?

Commonly used thresholds (discernability level)
\[ 0.1, \, 0.05, \, 0.01 \]


Note: these are also known as significance levels

\(\alpha = 0.05\)

For a discernability level of \(0.05\), we would conclude that since \(p < \alpha\), we have sufficient evidence to reject \(H_0\).


We would say that the data provides statistically discernable evidence against the null hypothesis.


Note: this is often phased as the data being statistically significant

Why \(0.05\)?

A discernability level of \(0.05\) is very common. Why is this?

https://www.openintro.org/book/stat/why05